Dependence in Observational Data

• Individuals are nested in social networks

  • Individual decisions are influenced by their friends.

• Provinces are surrounded by other provinces

  • Provinces mimic one another's policies

• Country-level outcomes are often a result of negotiations with other countries:

  • Economic or environmental policies

Three Mechanisms for Spatial Dependence

• Common exposure---similarity in outcomes is driven by an exogenous factor that affects nearby units (the effect of earthquakes on housing prices)

• Homophily---similarity in outcomes is endogenous, units are similar because they self-select into the same outcome (e.g., partisan geo-sorting)

• Diffusion---nearby units affect each other through learning, imitation, etc (e.g., policy diffusion)

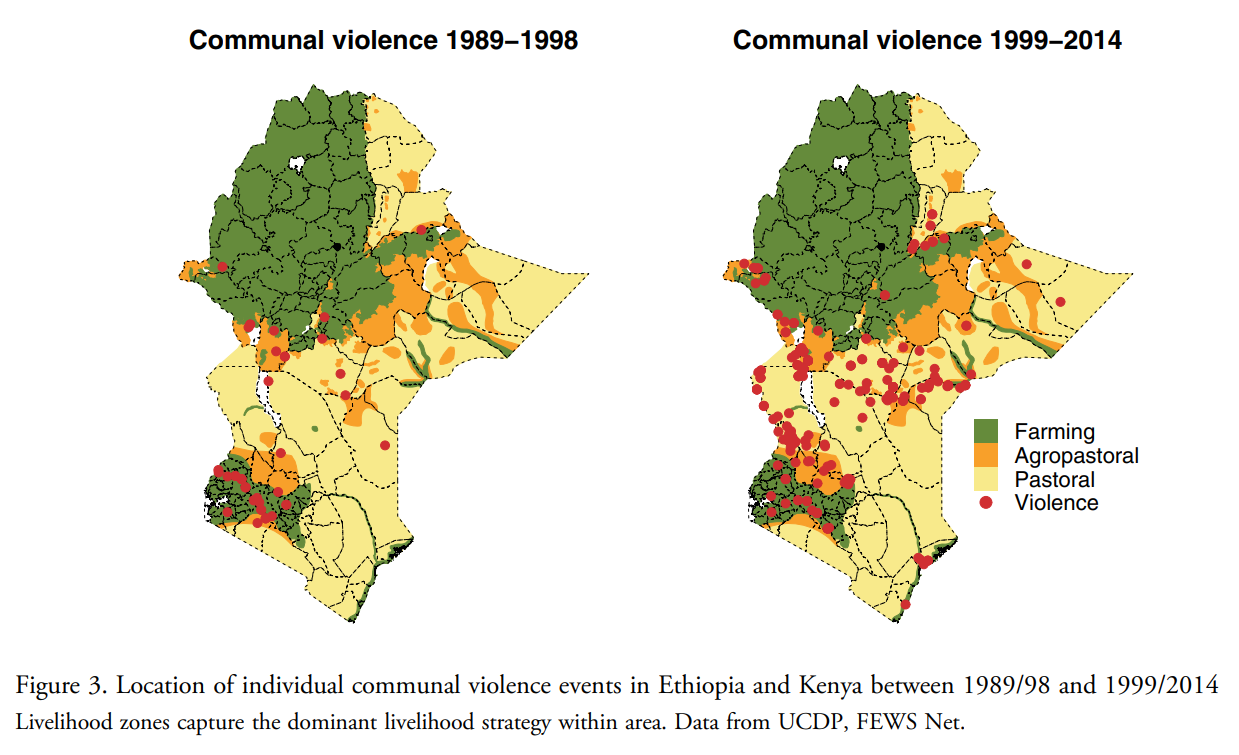
Source: van Weezel S. "On climate and conflict: Precipitation decline and communal conflict in Ethiopia and Kenya." Journal of Peace Research. 2019;56(4):514--528.

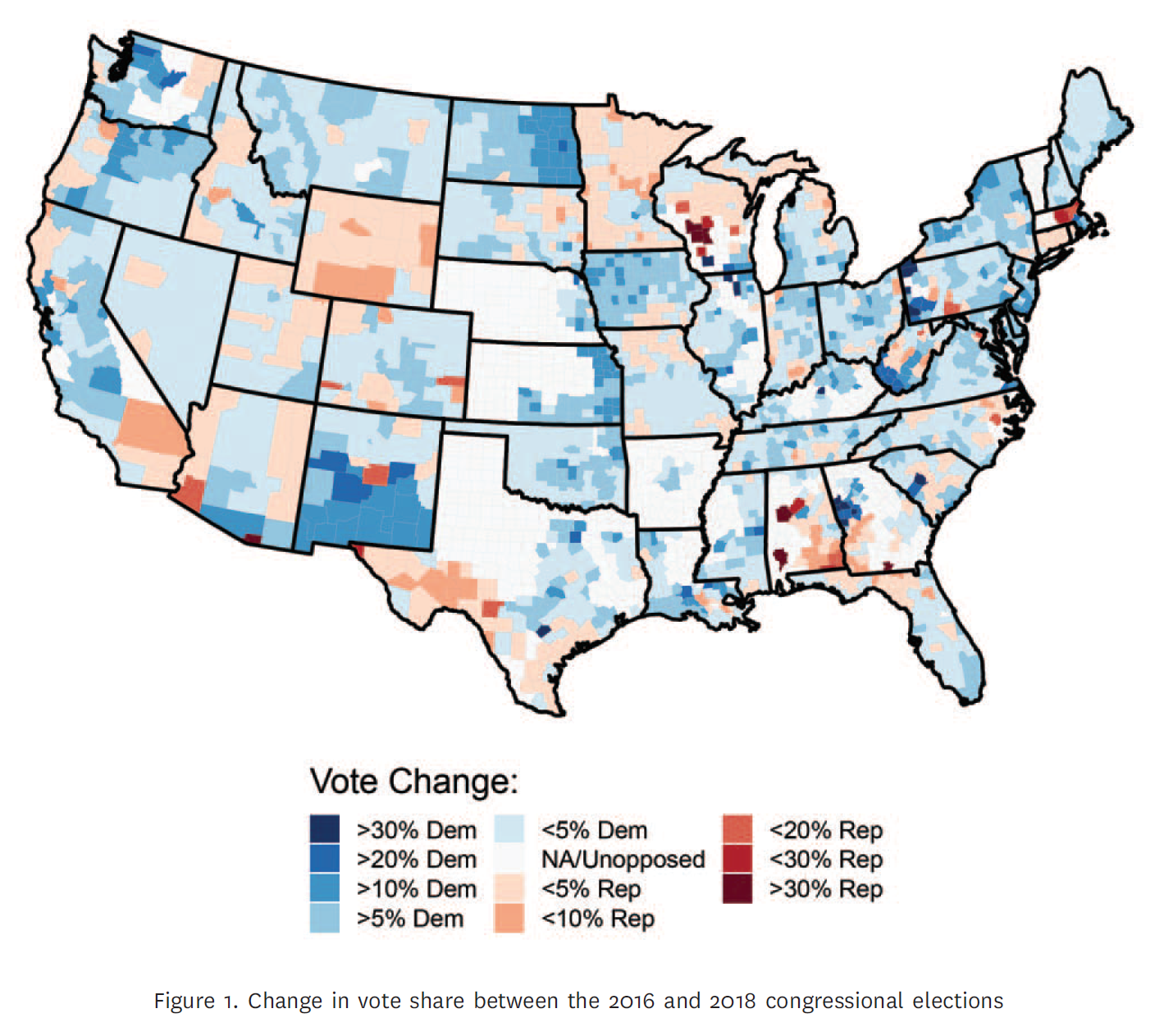
Source: Chyzh, Olga V. and R. Urbatsch. 2021. "Bean Counters: The Effect of Soy Tariffs on Change in Republican Vote Share Between the 2016 and 2018 Elections."Journal of Politics 83 (1): 415--419.

What Explains Variation in Covid-19 Cases?

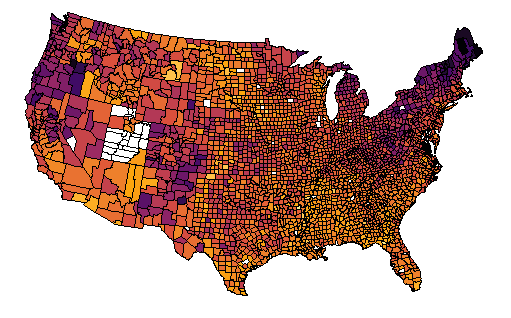
Common Exposure

Neighboring counties have similar Covid-19 rates because of their underlying similarities, e.g. demographics, political ideology (anti-mask sentiment), etc.

$$Covid19cases/ca{p}_i={\beta }_0+{\beta }_{1}Urba{n}_i+{\beta }_{2}Trump{16}_i+{\beta }_{3}medin{c}_i+u_i,$$

Homophily: Spatial X

Neighboring units tend to converge on outcomes because the causal variables (anti-vaccine sentiments) cluster by neighborhood locations (partisan geo-sorting).

$$Covid19cases/ca{p}_i={\beta }_0+{\beta }_{1}Urba{n}_i+{\beta }_{2}Trump{16}_i+{\beta }_{3}medin{c}_i+\rho \sum _{j\ne i}^N{w}_{ij}Trump{16}_j+u_i,$$ where $\rho$ is the estimation parameter for spatial dependence, and $w_{ij}$ measures whether $i$ and $j$ are neighbors.

• This is a spatial-X regression.

• $\sum _{j\ne i}^N{w}_{ij}Trump{16}_j$ is a spatially lagged independent variable measuring the average Trump support in neighboring counties.

• The coefficient $\rho$ is a measure of spatial homophily.

Contiguity Matrix W

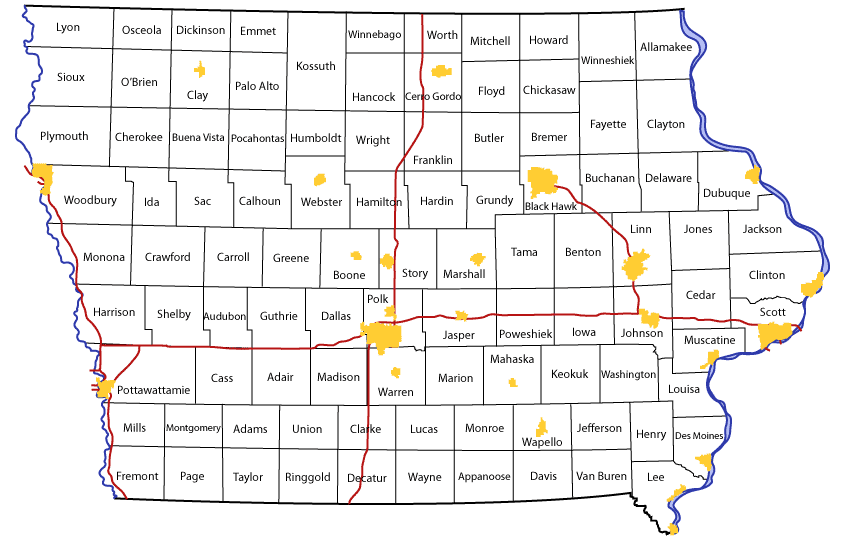
Contiguity Matrix W

##         Benton Linn Jones Iowa Johnson Cedar
## Benton       0    1     0    1       0     0
## Linn         1    0     1    0       1     1
## Jones        0    1     0    0       0     1
## Iowa         1    0     0    0       1     0
## Johnson      0    1     0    1       0     1
## Cedar        0    1     1    0       1     0

Row Standardized W

Divide by the row sum, so that each neighbor's influence decreases with the total number of neighbors.

##         Benton Linn Jones Iowa Johnson Cedar
## Benton    0.00 0.50  0.00 0.50    0.00  0.00
## Linn      0.25 0.00  0.25 0.00    0.25  0.25
## Jones     0.00 0.50  0.00 0.00    0.00  0.50
## Iowa      0.50 0.00  0.00 0.00    0.50  0.00
## Johnson   0.00 0.33  0.00 0.33    0.00  0.33
## Cedar     0.00 0.33  0.33 0.00    0.33  0.00

Diffusion: Spatial Y

$$Covid19cases/ca{p}_i={\beta }_0+{\beta }_{1}Urba{n}_i+{\beta }_{2}Trump{16}_i+{\beta }_{3}medin{c}_i+\rho \sum _{j\ne i}^N{w}_{ij}Covid19cases/ca{p}_j+u_i,$$ where $\rho$ is the estimation parameter for spatial dependence, and $w_{ij}$ measures whether $i$ and $j$ are neighbors.

• This is a spatial-Y regression.

• $\sum _{j\ne i}^N{w}_{ij}Covid19cases/ca{p}_j$ is a spatially lagged dependent variable measuring the average number of Covid-19 cases in neighboring counties.

• The coefficient $\rho$ is a measure of spatial dependence.

Spatial Y Model

$$\text{y}=\rho \text{W}\text{y}+\text{X}\beta \beta +ϵϵ,$$

• $\text{y}$ the dependent variable, is an N x 1 vector of cross sections stacked by period;

• $\rho$ is the spatial coefficient;

• $\text{W}$ is an N x N spatial-weighting matrix;

• $\text{X}$ contains N observations on k independent variables

• $\beta \beta$ is a k x 1 vector of coefficients;

• $ϵϵ$ is an N by 1 vector of stochastic components.

Spatial Y Model

$$\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\\ ⋮\\ y_N\end{array}\right]=\rho \left[\begin{array}{ccccc}0& W_{12}& W_{13}& \cdots & W_{1N}\\ W_{21}& 0& W_{23}& \cdots & W_{2N}\\ W_{31}& W_{32}& 0& \cdots & W_{3N}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ W_{N1}& W_{N2}& W_{N3}& \cdots & 0\end{array}\right]+\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1k}\\ x_{21}& x_{22}& \cdots & x_{2k}\\ ⋮& ⋮& \ddots & ⋮\\ x_{N1}& x_{N2}& \cdots & x_{Nk}\end{array}\right]\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_k\end{array}\right]+\left[\begin{array}{c}{ϵ}_1\\ {ϵ}_2\\ ⋮\\ {ϵ}_N\end{array}\right]$$

Spatial Lag Model

$$\text{y}=\rho \text{W}\text{y}+\text{X}\beta \beta +ϵϵ,$$

By re-arranging, can isolate y on the left-hand side:

$$\text{y}=[I_N{I}_N-\rho {\text{W}}_N{]}^{-1}\{\text{X}\beta \beta +ϵϵ\}$$

Likelihood

Other Types of Space

• Ideology

• International trade

• Alliances

• Other examples?

Example: Spatial X

mydata<-read.csv("./data/covid_data.csv", header=TRUE) 
mydata$trumpmarg[is.na(mydata$trumpmarg)]<-0
contigmat<-read.table("data/contigmat.txt") |> as.matrix()
contigmat1<-contigmat/apply(contigmat,1,sum) #row-standardize
mydata$W_trumpmarg<-contigmat1%*%mydata$trumpmarg
m1<-lm(data=mydata, cases_pc~urb2010+trumpmarg+medinc1317)
m2<-lm(data=mydata, cases_pc~urb2010+trumpmarg+medinc1317+W_trumpmarg)

Spatial Regression

library(spdep)
library(spatialreg)
contigmat<-read.table("./data/contigmat.txt") 
contigmat<-as.matrix(contigmat)
W1<-mat2listw(contigmat, row.names = NULL, style="W", zero.policy = TRUE)
summary(W1$neighbours)
W2<-nb2listw(W1$neighbours, glist=NULL, style="W", zero.policy=TRUE)
m3 <- lagsarlm(data=mydata, cases_pc~log(totpop1317)+urb2010+trumpmarg+medinc1317, W2, zero.policy=TRUE)
summary(m3)
saveRDS(m3,"m3.RDS")

Interpretation

Set up a hypothetical scenario:

• Expected change in Covid-19 cases that would result from increasing urbanization in Johnson county, IA

names<-c("benton","cedar","iowa","johnson","jones","linn")
mymat<-matrix(c(0,0,1,0,0,1,
                0,0,0,1,1,1,
                1,0,0,1,0,0,
                0,1,1,0,0,1,
                0,1,0,0,0,1,
                1,1,0,1,1,0),nrow=6,ncol=6)
dimnames(mymat)<-list(names,names)
mymat<-round(mymat/apply(mymat,1,sum),2)
d<-dplyr::filter(mydata, state=="IA" & county %in% names)

Set up A Comparison by Shocking One of the Units on X

m3<- readRDS("m3.RDS")
I<- diag(6)
X0<-as.matrix(cbind(1,log(d$totpop1317), d$urb2010, d$trumpmarg, d$medinc1317))
urb<-d$urb2010
urb[4]<-1
X1<-as.matrix(cbind(1,log(d$totpop1317), urb, d$trumpmarg, d$medinc1317))
A<-solve(I-coef(m3)[1]*mymat)
mycoef<-as.matrix(coef(m3))
Yhat0<- A%*%(X0%*%mycoef) #may need to remove first element of mycoeff[-1]; keep this for knitting (RDS works different)
Yhat1<- A%*%(X1%*%mycoef) #may need to remove first element of mycoeff[-1]
Y_ch<-Yhat1-Yhat0
sim<- cbind.data.frame(names,Y_ch)

Visualize the Effect

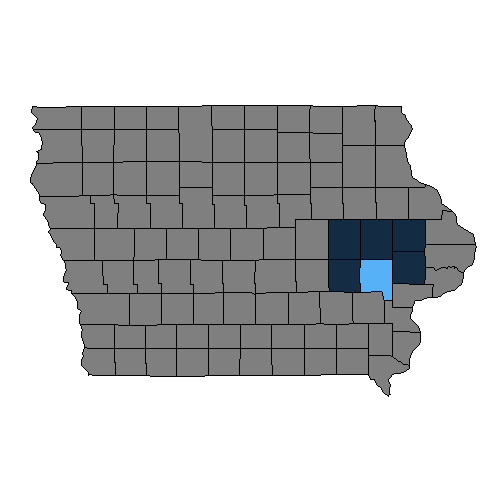
Your Turn

Suppose you want to test whether variable votech (the change in Republican vote share between the 2016 and 2018 Congressional election) is spatially clustered.

1. Calculate a measure of the average change in Republican vote share in neighboring states.

2. Estimate a model of votech as a function of urb2010, medinc1317, perc_HS_GED, perclatino1317 and trumpmarg.

3. Estimate the same model plus a the average change in Republican vote share in neighboring states.

Making Maps

library(tidyverse)
library(mapproj)
library(maps)
library(mapdata)
states <- map_data("state")
head(states)

##        long      lat group order  region subregion
## 1 -87.46201 30.38968     1     1 alabama      <NA>
## 2 -87.48493 30.37249     1     2 alabama      <NA>
## 3 -87.52503 30.37249     1     3 alabama      <NA>
## 4 -87.53076 30.33239     1     4 alabama      <NA>
## 5 -87.57087 30.32665     1     5 alabama      <NA>
## 6 -87.58806 30.32665     1     6 alabama      <NA>

What You Need

• Latitude/longitude points for all map boundaries

• Need to know to which boundary/state lat/long points belong

• Need to know the order to connect points within each group

A Basic (Rather Hideous) Map

library(ggplot2)
ggplot() +  geom_path(data=states, aes(x=long, y=lat, group=group),color="black", size=.5)

A Bit Nicer of a Map

#Set theme options:
theme_set(theme_grey() + theme(axis.text=element_blank(),
                               axis.ticks=element_blank(),
                               axis.title.x=element_blank(),
                               axis.title.y=element_blank(),
                               panel.grid.major = element_blank(),
                               panel.grid.minor = element_blank(),
                               panel.border = element_blank(),
                               panel.background = element_blank(),
                               legend.position="none"))
ggplot() +  geom_path(data=states, aes(x=long, y=lat, group=group),color="black", size=.5)+ coord_map()

Polygon instead of Path

ggplot() +  geom_polygon(data=states, aes(x=long, y=lat, group=group),color="black", size=.5)+ coord_map()

Incorporate Information About States

• Add other geographic information (e.g., counties) by adding geometric layers to the plot

• Add non-geographic information by altering the fill color for each state

  • Use geom = "polygon" to treat states as solid shapes to add color

  • Incorporate numeric information using color shade or intensity

  • Incorporate categorical informaion using color hue

Categorical Information Using Hue

If a categorical variable is assigned as the fill color then ggplot will assign different hues for each category.

Let’s load in a state regions dataset:

statereg<- read.csv("./data/statereg.csv")
head(statereg)

##        State StateGroups
## 1 california        West
## 2     nevada        West
## 3     oregon        West
## 4 washington        West
## 5      idaho        West
## 6    montana        West

Join the Data

states.class.map <- left_join(states, statereg, by = c("region" = "State"))
head(states.class.map)

##        long      lat group order  region subregion StateGroups
## 1 -87.46201 30.38968     1     1 alabama      <NA>       South
## 2 -87.48493 30.37249     1     2 alabama      <NA>       South
## 3 -87.52503 30.37249     1     3 alabama      <NA>       South
## 4 -87.53076 30.33239     1     4 alabama      <NA>       South
## 5 -87.57087 30.32665     1     5 alabama      <NA>       South
## 6 -87.58806 30.32665     1     6 alabama      <NA>       South

Plot the Regions

ggplot() +  geom_polygon(data=states.class.map, aes(x=long, y=lat, group=group, fill = StateGroups), colour = I("black"))+ coord_map()+theme(legend.position="bottom")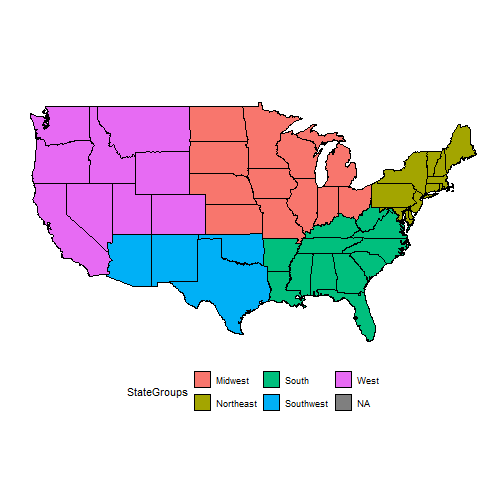

Your Turn

Use color to show the expected change in Covid-19 cases that result from increasing urbanization in Johnson county, IA on a map.

Your Turn (Advanced)

1. Read in the animal.csv data:

animal <- read.csv("./data/animal.csv")

1. Plot the location of animal sightings on a map of the region
2. On this plot, try to color points by class of animal and/or status of animal
3. Advanced: Could we indicate time somehow?